
Você sabe fazer comparação de frações?
Essa é uma habilidade trabalhada no ensino fundamental, mas saiba que ela é essencial para responder às questões de matemática do Enem.
As frações possuem o objetivo de representar partes de um inteiro através de situações geométricas ou numéricas. Comparar frações significa analisar qual representa a maior ou menor quantidade ou se elas são iguais.
Você sabe como fazer isso? Se sua resposta é não, continue neste artigo que falaremos tudo sobre comparação de frações e como esse conteúdo pode aparecer no Enem.
Aqui você vai ver:
De forma geral, podemos dizer que frações são representações matemáticas das partes de determinada quantidade que foram divididas em pedaços ou fragmentos iguais.
Parece um pouco abstrato, não é mesmo? Mas com o exemplo abaixo, vai ficar mais fácil de entender!
Imagine que Maria comprou uma pizza e dividiu em 4 fatias iguais. Como não estava com muita fome, ela comeu apenas uma fatia. Que fração da pizza Maria comeu?
Se havia 4 fatias de pizza e Maria comeu apenas uma, podemos dizer que ela ingeriu 1 pedaço de 4 da pizza.
Assim, a fração que representa a quantidade de pizzas que Maria comeu seria:

O número 1 representa o numerador da fração e indica quantas partes foram tomadas – no caso do nosso exemplo, quantos pedaços foram comidos por Maria.
Já o número 4, representa o denominador da fração e indica em quantas partes o todo foi dividido — ou seja, em quantas partes a pizza estava dividida.
Esse é um exemplo de como as frações estão presentes em nosso dia a dia.
Elas são úteis em várias situações como a que mostramos acima, principalmente para representar algo que não conseguimos apresentar através de números naturais.
Agora que você já sabe o que é uma fração, vamos ao que interessa: comparação de frações!
Comparação de frações significa estabelecer uma regra de igualdade ou desigualdade entre elas.
Você lembra que as frações possuem o objetivo de representar partes de um número inteiro por meio de situações geométricas ou numéricas, certo?
Então, comparar significa analisar qual representa a maior ou menor quantidade ou se elas são iguais
Podemos comparar frações utilizando a representação numérica através de algumas técnicas e propriedades. Abaixo, apresentamos as principais:
O primeiro passo para comparar frações é sempre observar o denominador. Lembre-se que denominador é o número de baixo da fração e o numerador, o de cima.
Se o denominador das frações for o mesmo, você só precisa olhar o numerador para saber qual é maior.
Por exemplo, com as frações 5/12 e 7/12, você sabe que 7/12 é maior que 5/12 porque 7 é maior que 5.
Assim, para comparar frações de mesmo denominador, a estratégia é sempre observar o numerador.
🔵Leia também: Como calcular a nota do Enem: um guia prático para saber sua média
Já quando duas frações tiverem o mesmo numerador, a maior é aquela que tem o menor denominador.
Por exemplo, com as frações 1/4 e 1/5, você sabe que 1/4 é maior.
Mas e quando as frações têm numeradores e denominadores diferentes?
Nesse caso, é preciso igualar os denominadores com frações equivalentes, seja por um múltiplo qualquer ou pelo mmc.
Observe o exemplo abaixo retirado do portal do professor Kelven Lima. Vamos comparar 5/6 e 8/9:
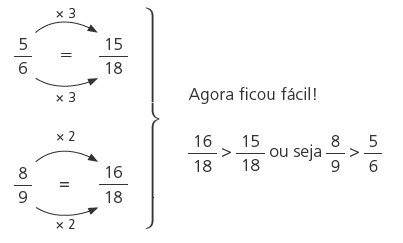
Uma outra maneira de fazer comparações entre frações é multiplicar o denominador de uma fração pelo numerador da outra, comparando os resultados obtidos.
Vejamos esse macete com o mesmo exemplo:
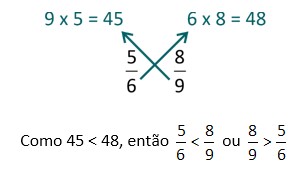
🔵Leia também: Pontuação do Enem: quanto precisa alcançar para entrar na faculdade?
Agora que você já sabe como fazer comparação de frações, que tal colocar em prática seus conhecimentos?
Abaixo, selecionamos algumas questões do Enem que envolvem comparação de frações. Confira:
1 - (Enem PPL 2020) A fim de reforçar o orçamento familiar, uma dona de casa começou a produzir doces para revender. Cada receita é composta de 4/5 de quilograma de amendoim e 1/5 de quilograma de açúcar.
O quilograma de amendoim custa R$ 10,00 e o do açúcar, R$ 2,00. Porém, o açúcar teve um aumento e o quilograma passou a custar R$ 2,20. Para manter o mesmo custo com a produção de uma receita, essa dona de casa terá que negociar um desconto com o fornecedor de amendoim.
Nas condições estabelecidas, o novo valor do quilograma de amendoim deverá ser igual a
✅Gabarito: E
2 - (Enem 2017) Em uma cantina, o sucesso de vendas no verão são sucos preparados à base de polpa de frutas. Um dos sucos mais vendidos é o de morango com acerola, que é preparado com 2/3 de polpa de morango e 1/3 de polpa de acerola. Para o comerciante, as polpas são vendidas em embalagens de igual volume. Atualmente, a embalagem da polpa de morango custa R$ 18,00 e a de acerola, R$ 14,70. Porém, está prevista uma alta no preço da embalagem da polpa de acerola no próximo mês, passando a custar R$ 15,30. Para não aumentar o preço do suco, o comerciante negociou com o fornecedor uma redução no preço da embalagem da polpa de morango. A redução, em real, no preço da embalagem da polpa de morango deverá ser de:
✅Gabarito: E
3 - (Enem 2016) Nas construções prediais são utilizados tubos de diferentes medidas para a instalação da rede de água. Essas medidas são conhecidas pelo seu diâmetro, muitas vezes medido em polegada. Alguns desses tubos, com medidas em polegada, são os tubos de 1/2, 3/8 e 5/4.
Colocando os valores dessas medidas em ordem crescente, encontramos
✅Gabarito: C
2023 © BLOG DO EAD | Todos os Direitos Reservados