
Uma maneira de estudar matemática e facilitar a solução de questões exatas é através de representações gráficas.
Um exemplo é o Diagrama de Venn, que é amplamente utilizado no estudo de conjuntos.
Ele é uma forma visual e simples de representar relações entre diferentes conjuntos, o que torna mais fácil o entendimento de quem possui maior dificuldade de lidar com números.
Dessa maneira, o aluno que está se preparando para a prova de matemática do Enem consegue organizar seu plano de estudo de uma maneira que facilite a melhor compreensão da matéria.
Mas você sabe como o Diagrama de Venn funciona e quais são as operações que derivam deste método? Então, siga acompanhando!
Você vai conferir:
O Diagrama de Venn é um método para representarmos conjuntos numéricos de forma geométrica.
É uma representação gráfica, ou seja, um desenho técnico. Essa representação facilita a visualização e realização das operações entre conjuntos.
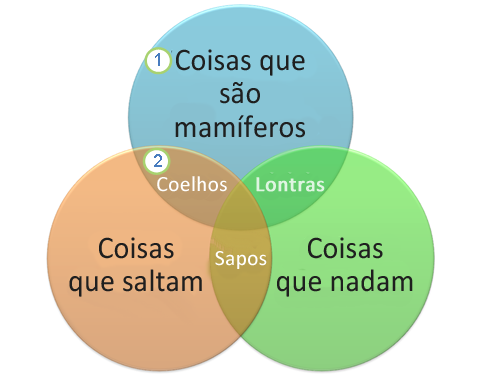
Na imagem: exemplo de como o Diagrama de Venn funciona. Fonte: Suport Microsoft
O diagrama de Venn recebe esse nome em homenagem ao matemático britânico John Venn (1834-1923) e é mais famoso por ser aplicado na matemática, principalmente na matéria de Conjuntos Numéricos.
Contudo, ele também é utilizado na lógica e na identificação de dados sociais ou de mercado.
O método ainda pode ser chamado de Diagrama de Venn-Euler ou Diagrama de Conjunto.
O Diagrama é formado por um círculo, que formam números dentro de sua área, fazendo com que uma destas representações geométricas contemplem um determinado conjunto.
Quando ocorrem cruzamentos entre esses círculos e eles se encontram, as áreas que se cruzam são denominadas como subconjuntos.
O Diagrama de Venn utiliza representações gráficas para ilustrar as relações lógicas matemáticas entre dois ou mais conjuntos.
Na maioria dos casos, matemáticos se utilizam desses recursos para organizar graficamente a estrutura cognitiva do pensamento matemático e destacar os elementos que são diferentes e semelhantes nas equações em que estão trabalhando
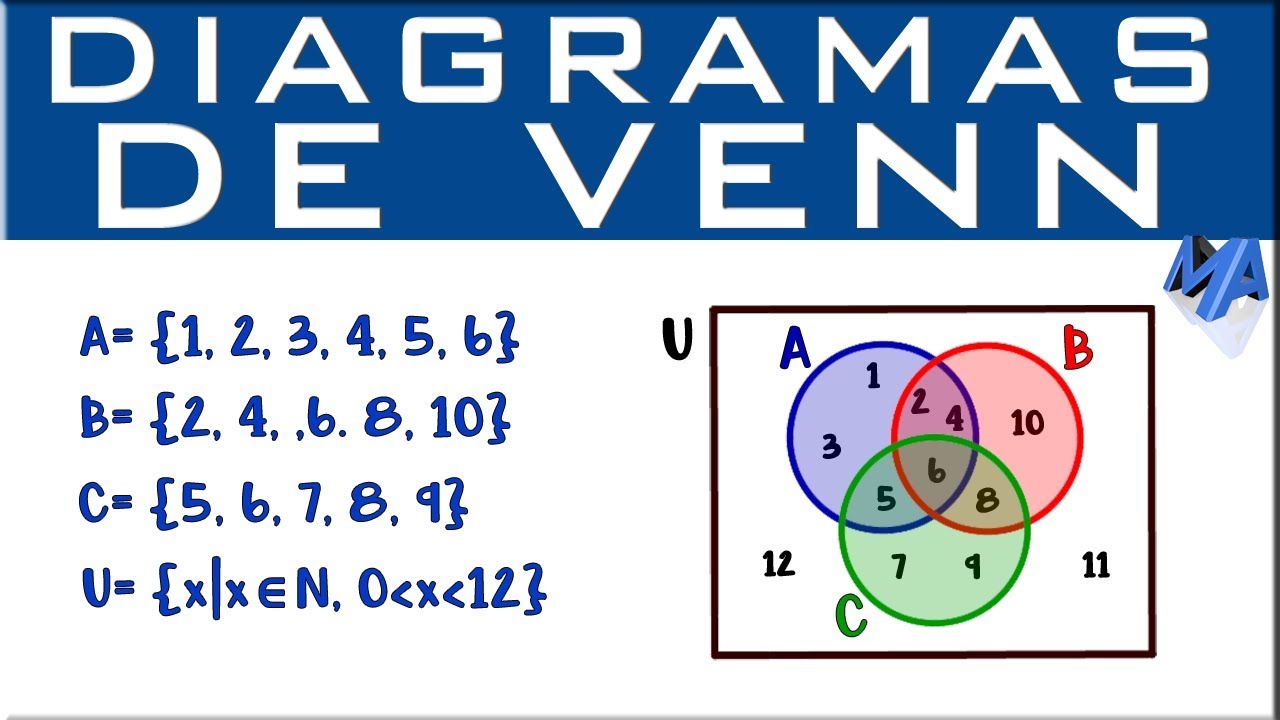
Imagem: exemplo de Diagrama de Venn com conjuntos numéricos. Fonte: Matemáticas profe Alex
Na representação gráfica do Diagrama de Venn, o Universo é demonstrado como um retângulo, para que seja visto como um ambiente repleto de possibilidades.
Nele, estão contidos os conjuntos e outros elementos externos, que fazem parte do Universo, mas que não pertencem aos círculos.
Vamos entender melhor esses exemplos abaixo, quando conhecermos os tipos de conjuntos.
Para o estudante que está se preparando para o Enem, conhecer melhor o diagrama ajuda na resolução de questões de lógica ou que envolvem interpretação de dados, como gráficos e porcentagens.
Confira abaixo os tipos de conjuntos no Diagrama de Venn:
O conjunto único é formado por um único círculo que contém um singular agrupamento de números.
Por exemplo, se tenho uma sacola com seis laranjas, e cada uma está enumerada de 1 a 6, meu conjunto é A = {1,2,3,4,5,6,} e sua representação no diagrama seria os números dentro de um círculo.
Esse conjunto é formado por elementos que não possuem relação e não se tocam em nenhum momento na representação gráfica.
São dois conjuntos distintos, com dois círculos separados.
Os conjuntos disjuntos possuem, como definição, serem formados pelos elementos que não estão em comum em nenhum dos dois conjuntos.
A relação de pertinência observa se o elemento pertence ou não a um determinado conjunto.
O símbolo de pertinência é marcado através dessa letra (∈) e quando o elemento não pertence ao conjunto, o símbolo recebe um traço (∉) e fica fora do diagrama.
A relação de inclusão verifica se um objeto está ou não dentro de outro conjunto. É uma maneira de analisar a relação entre os subconjuntos.
A partir da definição de se está contido (⊂), não está contido (⊂/), contém (⊃) ou não contém (⊃/), é que se observa se os elementos estão dentro dos conjuntos ou não.
Os elementos complementares não fazem parte dos conjuntos ou subconjuntos, mas estão presentes no Universo.
São elementos extras, representados no cantinho do retângulo.
Esses elementos normalmente são aqueles que não estão contemplados nos conjuntos observados, mas de alguma forma, por exemplo, em uma pesquisa, ainda assim fazem parte do universo analisado.
🔵Leia também: Como calcular a nota do Enem: um guia prático para saber sua média
Na matemática, qualquer operação pode significar um procedimento que utilize lógica e raciocínio, porém ainda seguem determinadas regras e procedimentos.
Nas operações entre conjuntos, essa máxima não é diferente.
Mas o que se configura por um conjunto? Pode ser descrito como um grupo ou uma coleção de elementos (números, letras, símbolos etc.), condicionados a uma determinada relação.
As operações básicas entre dois ou mais conjuntos são 3: União, Intersecção e Diferença.
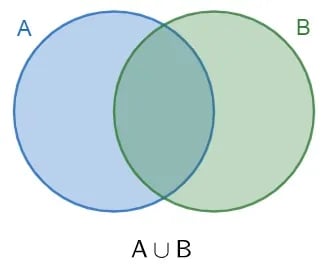
Fonte: Mundo Educação
A união é uma operação em que os elementos dos conjuntos são somados.
Nesse caso, cada conjunto é apresentado com os elementos que o compõem e na operação de união os dois conjuntos se fundem, formando um novo conjunto.
Porém, deve-se ter o cuidado na soma de conjuntos com elementos iguais, pois não é possível somar elementos repetidos duas vezes.
Esse elemento é então representado individualmente no meio da intersecção (ou soma) dos conjuntos.
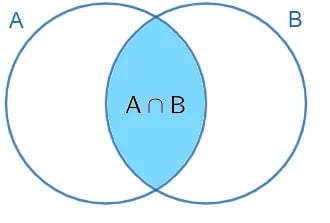
Fonte: Mundo Educação
A Intersecção é um novo conjunto numérico formado somente por elementos que pertencem a outros conjuntos ao mesmo tempo.
Assim, a intersecção de conjuntos refere-se aos elementos que se repetem.
Fonte: Mundo Educação
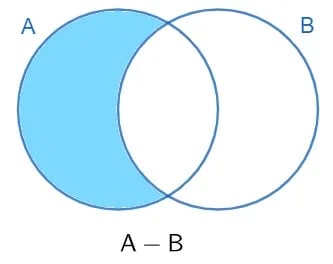
A diferença entre conjuntos corresponde aos elementos de um conjunto que não estão no outro conjunto.
Assim, esta operação elimina todos os elementos de um dos conjuntos. Ou seja, elimina os elementos que pertencem a A e não pertencem a B. É indicado por A - B.
2023 © BLOG DO EAD | Todos os Direitos Reservados