Funções matemáticas: o que são e como são cobradas no Enem?

As funções são expressões matemáticas que se caracterizam pela relação entre dois conjuntos numéricos. 

Cada função pode ser expressa por meio de um gráfico. E, como sabemos por aqui, os gráficos são presença confirmada no Enem. 

Pensando nisso, preparamos este artigo para te ajudar a entender funções de uma vez por todas e ver como elas costumam ser cobradas na prova de matemática do exame. 

Confira a lista abaixo e acompanhe a leitura:

O que mais cai em matemática no Enem?

O que são funções matemáticas

Elementos de uma função matemática

Os tipos de função matemática

Função constante

Função par

Função ímpar

Funções elementares: algébricas

Função afim ou polinomial do primeiro grau

Função Linear

Função do primeiro grau crescente

Função do primeiro grau decrescente

Função quadrática ou polinomial do segundo grau

Função raiz

Funções elementares: transcendentais

Função exponencial

Função logarítmica

Funções trigonométricas

Função modular

Passo a passo para resolver uma função matemática

Questões de funções matemáticas que caíram no Enem para você praticar

Conclusão

O que mais cai em matemática no Enem? 

De acordo com o último levantamento feito pelos organizadores da Coletânea Enem, as Grandezas Proporcionais e Médias Algébricas estão entre os temas mais frequentes e representam 19,4% das questões da prova. 

Em segundo lugar ficam os Problemas de 1° e 2° graus, que abrangem 15,6% do exame.  

Em terceiro lugar estão Porcentagem e Matemática Financeira, englobando 7,2% da prova.  

Confira a relação completa dos temas específicos mais recorrentes:

• Funções (6,7%)
• Noções básicas de estatística (6,1%)
• Probabilidade (5,0%)
• Análise combinatória (4,4%)
• Circunferências (3,3%)
• Equações do segundo grau e inequações (3,3%)
• Logaritmos (2,8%)
• Áreas de figuras planas e polígonos (2,2%) 
• Funções trigonométricas (seno e cosseno) (2,2%)
• Sequências numéricas (2,2%) 
• Cilindros (2,2%)
• Geometria espacial (2,2%)
• Potenciação e conjuntos numéricos (1,7%) 
• Cônicas e gráficos relacionados (1,7%) 
• Retas (1,6%)
• Aritmética (1,1%)
• Prismas, pirâmides e poliedros de Platão (1,1%)
• Matrizes (1,1%)
• Triângulos e polígonos regulares (1,1%)
• Geometria analítica (0,6%)
• Função e equações exponenciais (0,6%) 
• Geometria plana e trigonometria (0,6%)
• Ângulos (0,6%)
• Senos e cossenos (0,6%)

Todos estes conteúdos são retirados diretamente da Matriz de Referência do Enem, que orienta os conteúdos abordados em cada prova do exame. 

Dentre as sete competências cobradas na Prova de Matemática, a 5ª e a 6º dizem respeito a conhecimentos que podem envolver funções.

 Competência de área 5 - Modelar e resolver problemas que envolvem variáveis socioeconômicas ou técnico-científicas, usando representações algébricas.

• H19 - Identificar representações algébricas que expressem a relação entre grandezas.
• H20 - Interpretar gráfico cartesiano que represente relações entre grandezas.
• H21 - Resolver situação-problema cuja modelagem envolva conhecimentos algébricos.
• H22 - Utilizar conhecimentos algébricos/geométricos como recurso para a construção de argumentação.
• H23 - Avaliar propostas de intervenção na realidade utilizando conhecimentos algébricos.

Competência de área 6 - Interpretar informações de natureza científica e social obtidas da leitura de gráficos e tabelas, realizando previsão de tendência, extrapolação, interpolação e interpretação.

• H24 - Utilizar informações expressas em gráficos ou tabelas para fazer inferências.
• H25 - Resolver problema com dados apresentados em tabelas ou gráficos.
• H26 - Analisar informações expressas em gráficos ou tabelas como recurso para a

construção de argumentos.

O que são funções matemáticas

Uma função é a relação entre dois conjuntos numéricos (A e B), onde todos os elementos do grupo A se associam a um único elemento do grupo B.

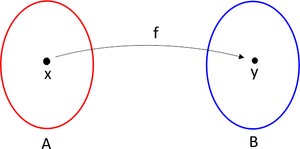
Imagem: Reprodução / Colégio QI

Na expressão que representa a função (f: A --> B), f é o nome da função, A é chamado de domínio e B é denominado de contradomínio. 

Na linguagem matemática, “f: A --> B” quer dizer “f de A em B”. 

Já “y = f(x)” expressa a lei de correspondência dos elementos dos grupos A e B, onde x é A e y é o conjunto B.

Elementos de uma função matemática 

As funções matemáticas, das mais simples até as mais complexas, são compostas por três elementos básicos. São eles: domínio, imagem e contradomínio. 

• O domínio (D) de uma função corresponde ao conjunto original (A), ou seja, o lugar “de onde partem as flechas”. 
• Os elementos do segundo grupo (B) que são “atingidos pelas flechas” representam a imagem (Im), também chamado de “conjunto de chegada”.
• Todos os elementos de B, que podem estar em relação ou não com o grupo A, são chamados de contradomínio.

Importante: nem todos os elementos do conjunto B precisam ser utilizados para que se configure uma função.

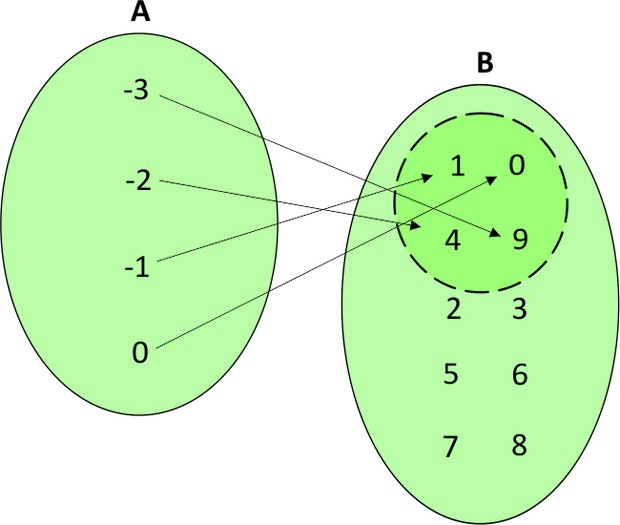
Imagem: Reprodução / Colégio QI

Função sobrejetora ou sobrejetiva: quando o conjunto imagem for igual ao conjunto do contradomínio, ou seja, possuem os mesmos elementos. Portanto, todo elemento de B é imagem de pelo menos um elemento de A.

Imagem: Reprodução / Colégio QI

Função injetora ou injetiva: quando, para quaisquer elementos x1 ≠ x2, temos f(x1) ≠ f(x2)

Imagem: Reprodução / Colégio QI

Bijetora ou bijetiva: quando ela for injetora e sobrejetora simultaneamente.

Imagem: Reprodução / Colégio QI

Casos em que a relação entre conjuntos não é considerada uma função:

1. Todos os elementos de A precisam estar em relação com B. Ou seja, quando há um ou mais elementos do Grupo A que não estão conectados com o Grupo B, a relação não é considerada função.
2. Os elementos de A só podem se relacionar com um elemento do grupo B de cada vez. Ou seja, quando um elemento de A está conectado com mais de um elemento em B, a relação também não é considerada função.
   
   

Os tipos de função matemática

Toda função pode ser expressa por uma fórmula ou por um gráfico. Desse modo, cada tipo de função tem suas representações específicas.

No universo da matemática, existem dezenas e dezenas de funções. Mas aqui veremos aquelas abordadas no Enem, que correspondem ao conteúdo de funções visto no ensino médio.

Função constante 

Na função constante, todo valor do domínio (x) tem a mesma imagem (y).

Fórmula geral da função constante:

f(x) = c

• x = Domínio
• f(x) = Imagem
• c = constante, que pode ser qualquer número do conjunto dos reais.

Gráfico da função constante: f(x) = 2

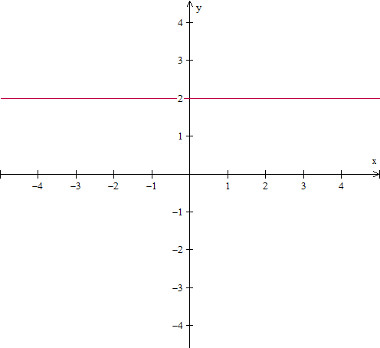Imagem: Reprodução / Mundo Educação

Função par

A função par é considerada simétrica em relação ao eixo vertical, porque ao dividi-la em partes iguais e sobrepô-las, as partes coincidem-se perfeitamente.

Fórmula geral da função par:

f(x) = f(- x)

• x = domínio
• f(x) = imagem
• - x = simétrico do domínio

Exemplo de gráfico da função par: f(x) = x2

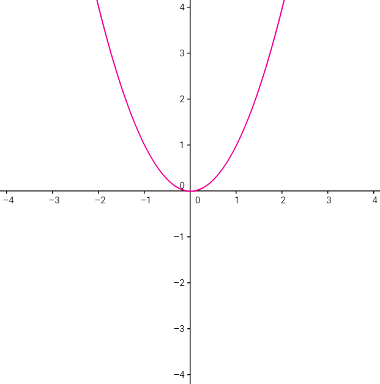
Imagem: Reprodução / Mundo Educação

Função ímpar

A função ímpar é simétrica (figura/gráfico que, ao dividi-la em partes iguais e sobrepô-las, as partes coincidem-se perfeitamente) em relação ao eixo horizontal, ou seja, à abscissa x.

Fórmula geral da função ímpar

f(– x) = – f(x)

• – x = domínio
• f(– x) = imagem
• - f(x) = simétrico da imagem

Exemplo de gráfico da função ímpar: f(x) = 3x

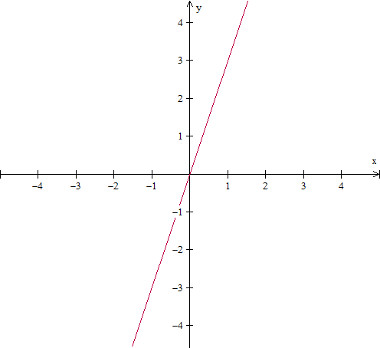
Imagem: Reprodução / Mundo Educação

Funções elementares: algébricas 

Função afim ou polinomial do primeiro grau

Uma função polinomial do primeiro grau possui o maior grau da variável x (termo desconhecido), sempre igual a 1. Nessa função, o gráfico é uma reta. 

Elementos que caracterizam a função: domínio x, imagem f(x) e coeficientes a e b.

Fórmula geral da função afim ou polinomial do primeiro grau

f(x) = ax + b

• x = domínio
• f(x) = imagem
• a = coeficiente
• b = coeficiente

Gráfico da função polinomial do primeiro grau: f(x) = 4x + 1

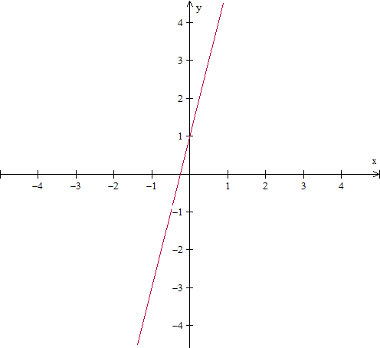
Imagem: Reprodução / Mundo Educação

Função Linear

A função linear tem sua origem na função do primeiro grau (f(x) = ax + b). 

Trata-se de um caso particular, onde b sempre será igual a zero.

Fórmula geral da função linear

f(x) = ax

• x = domínio
• f(x) = imagem
• a = coeficiente

Gráfico da função linear: f(x) = -x/3

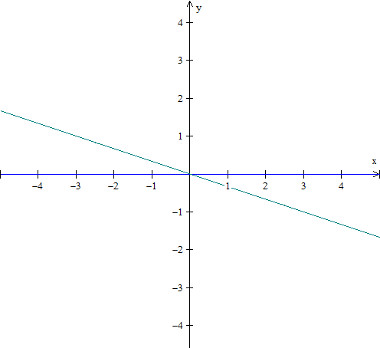
Imagem: Reprodução / Mundo Educação

Função do primeiro grau crescente

A função polinomial do primeiro grau é crescente sempre que o coeficiente “a” for diferente de zero e maior que um (a > 1).

Fórmula geral da função crescente

f(x) = + ax + b

• x = domínio
• f(x) = imagem
• a = coeficiente sempre positivo
• b = coeficiente

Gráfico da função do primeiro grau crescente: f(x) = 5x

Imagem: Reprodução / Mundo Educação

Função do primeiro grau decrescente

Na função decrescente, o coeficiente “a” da função do primeiro grau (f(x) = ax + b) é sempre negativo.

Fórmula geral da função decrescente

f(x) = - ax + b

• x= domínio/ incógnita

• f(x) = imagem
• - a = coeficiente sempre negativo
• b = coeficiente

Gráfico da função decrescente: f(x) = - 5x

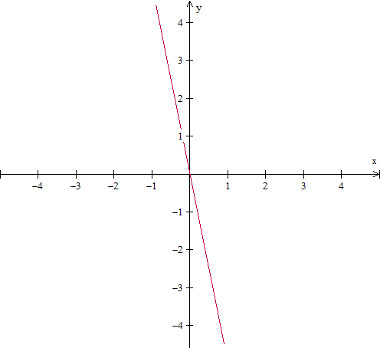
Imagem: Reprodução / Mundo Educação

Função quadrática ou polinomial do segundo grau

Dizemos que uma função é do segundo grau quando o maior expoente que acompanha a variável x (termo desconhecido) é 2. 

• O gráfico da função polinomial do segundo grau sempre será uma parábola. 
• Sua concavidade muda de acordo com o valor do coeficiente “a”.
• Quando “a” é positivo, a concavidade é para cima e, se for negativo, é para baixo.

Fórmula geral da função quadrática ou polinomial do segundo grau

f(x) = ax2 + bx + c

• x = domínio
• f(x) = imagem
• a = coeficiente que determina a concavidade da parábola
• b = coeficiente
• c = coeficiente

Gráfico da função polinomial do segundo grau: f(x) = x2 – 6x + 5

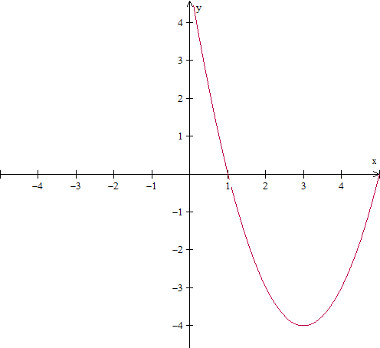
Imagem: Reprodução / Mundo Educação

Função raiz

O domínio da função raiz é o termo “n”, que faz parte do expoente. 

Por isso, se n for ímpar, o domínio (x) será o conjunto dos números reais. E se n for par, o domínio (x) será somente os números reais positivos. Afinal, quando o índice é par, o radicando (termo que fica dentro da raiz) não pode ser negativo.

Fórmula geral da função raiz

f(x) = x 1/n

• f(x) = Imagem
• x = domínio/ base
• 1/n = expoente

Exemplo de gráfico da função raiz: f(x) = (x)1/2

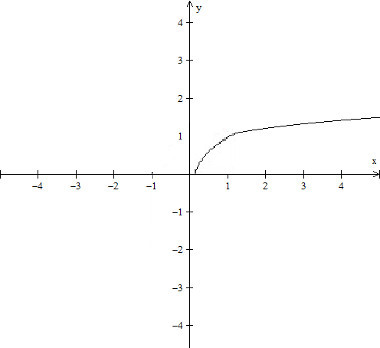
Imagem: Reprodução / Mundo Educação

Funções elementares: transcendentais 

Função exponencial

Dizemos que uma função é exponencial quando a variável “x” estiver no expoente em relação à base de um termo numérico ou algébrico.

• Caso esse termo seja maior que 1, o gráfico da função exponencial é crescente.
• Caso o termo for um número entre 0 e 1, o gráfico da função exponencial é decrescente.

Fórmula geral da função exponencial

f(x) = ax

• a > 1 ou 0 < a < 1
• x = domínio
• f(x) = imagem
• a = Termo numérico ou algébrico

Gráfico da função exponencial crescente: f(x) = (2)x, para a = 2

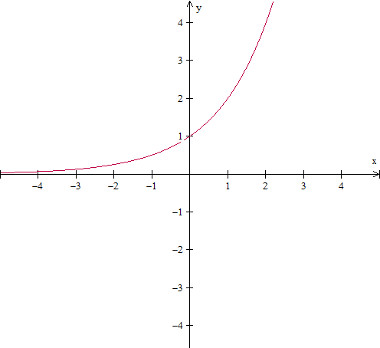
Imagem: Reprodução / Mundo Educação

Exemplo de gráfico da função exponencial decrescente: f(x) = (1/2)x para a = ½

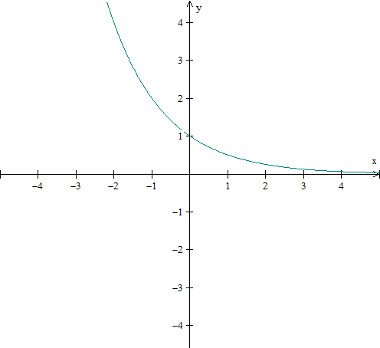
Imagem: Reprodução / Mundo Educação

Função logarítmica

Na função logarítmica, o domínio é o conjunto dos números reais maiores que zero, enquanto o contradomínio é o conjunto dos elementos dependentes da função, sendo todos números reais.

Fórmula geral da função logarítmica

f(x) = loga x

• a = base do logaritmo
• f(x) = Imagem/ logaritmando

• x = Domínio/ logaritmo

Gráfico da função logarítmica: f(x) = log10 (5x - 6)

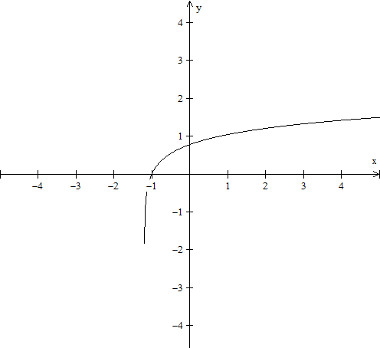
Imagem: Reprodução / Mundo Educação

Funções trigonométricas

As funções trigonométricas, também chamadas de funções angulares, são utilizadas para o estudo dos triângulos e em fenômenos periódicos. Descrevem a razão de coordenadas dos pontos de um círculo unitário. 

Principais funções:

• Seno: f(x) = sen x
• Cosseno: f(x) = cos x
• Tangente: f(x) = tg x

Gráfico da função trigonométrica seno: f(x) = sen (x + 2)

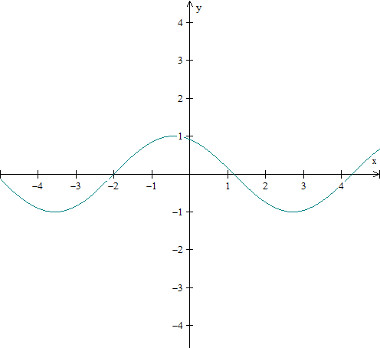
Imagem: Reprodução / Mundo Educação

Exemplo de gráfico da função trigonométrica cosseno: f(x) = cos (x + 2)

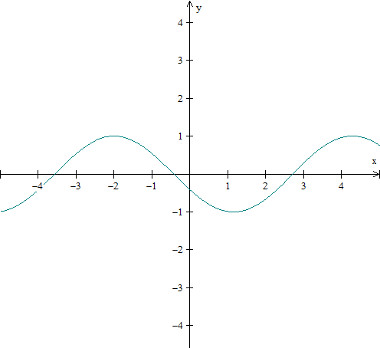
Imagem: Reprodução / Mundo Educação

Exemplo de gráfico da função tangente: f(x) = tg (x + 2)

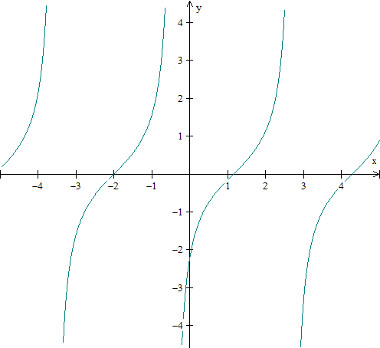
Imagem: Reprodução / Mundo Educação

Funções especiais: básicas 

Função modular

A função modular é caracterizada pelo módulo, valor absoluto de um número representado por (| |). Seu valor pode ser obtido tanto negativo quanto positivo. 

Exemplo: 

|x| = + x 

ou 

|x| = - x

Fórmula geral da função modular

f(x) = x, se x≥ 0

ou

f(x) = – x, se x < 0

• x = domínio
• f(x) = imagem
• - x = simétrico do domínio

Gráfico da função modular: f(x) =

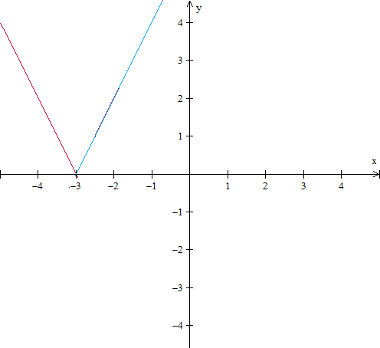
Imagem: Reprodução / Mundo Educação

Passo a passo para resolver uma função matemática 

Cada função tem sua maneira de resolver. O que importa é entender o modo como cada uma funciona e praticar bastante depois de entender cada uma delas.

Clique aqui para conferir uma aula sobre como resolver funções.

Questões de funções matemáticas que caíram no Enem para você praticar

Como vimos no início deste artigo, os diferentes tipos de funções são bastante cobrados no Enem. 

Por isso, é importante que você faça muitos exercícios para saber identificar as fórmulas de cada função e arrasar nos cálculos lá no dia da prova de matemática do Enem. 

Fique de olho nas listas de exercícios que indicamos para você:

Tipos de funções

Funções trigonométricas

Equações e funções polinomiais do 1º grau

Equações e funções polinomiais do 2º grau

Conclusão

Agora que você está por dentro dos tipos de funções que caem no Enem, não esqueça que o segredo é praticar bastante o conteúdo com base em questões antigas do exame.

Para otimizar seus estudos, confira as dicas da Univali sobre como montar um plano de estudos mais eficiente para a sua jornada pré-vestibular.

Confira ainda:

• Lista de exercícios resolvidos de matemática 
• Como atingir a nota 1000 na redação do Enem

Ah! Com a sua nota do Enem, você pode obter bolsa de até 100% na Univali EAD, uma universidade com 55 anos de experiência no mercado e 90% de empregabilidade dos alunos formados.

Bons estudos!