
A prova de matemática do Enem é uma das mais temidas pelos estudantes. Afinal, ela reúne uma série de conhecimentos da área que podem parecer difíceis de aprender até a data do exame.
Por isso, conhecer o que mais cai em matemática no Enem pode facilitar e tornar o seu estudo muito mais eficaz.
Existe uma série de conteúdos que são cobrados todos os anos no Enem. Sendo assim, focar nesses conhecimentos pode ser uma boa estratégia para dar conta de todas as matérias e estar bem preparado para o dia da prova.
Neste artigo, trazemos o que mais cai em matemática no Enem e explicamos como se preparar para essa etapa do Enem.
Aqui você vai conferir:
O Enem (Exame Nacional do Ensino Médio) acontece todos os anos no Brasil desde 1998. Ele foi criado para ser uma métrica da qualidade do ensino médio do país, porém hoje se transformou na principal porta de entrada para o ensino superior.
A prova reúne conteúdos do ensino médio divididos em quatro grandes áreas do conhecimento. Confira:
Cada uma das provas conta com 45 perguntas objetivas, resultando em 180 questões ao todo.
Diferente das outras provas, as questões de Matemática e Suas Tecnologias não abordam mais de uma disciplina, apenas matemática.
Todas as questões são de múltipla escolha, contendo 5 alternativas, e apresentam um enunciado que contextualiza a pergunta.
É discutido entre candidatos do Enem que apenas saber regra de três já ajuda a navegar pela prova de Matemática e suas Tecnologias, porém não leve essa conversa tão a sério e estude os conteúdos mais recorrentes.
Também preste bastante atenção ao enunciado da questão, pois ele pode ajudar a evitar pegas-ratão ou, até mesmo, já conter a resposta.
🔵 Leia também: Quantos pontos precisa para passar no ENEM?
Você pode conferir todas as matérias que caem na prova na Matriz de Referência do Enem, um documento elaborado pelo MEC.
Porém, para facilitar o acesso, vamos comentar aqui os assuntos que mais caíram na prova de Matemática e suas Tecnologias nos últimos anos.
Este assunto engloba os conteúdos de regra de três, razão e proporção, porcentagem e escalas.
Grandezas proporcionais é um assunto recorrente no Enem e aquele que mais contém questões. Isso porque este é um assunto que lidamos no dia a dia com frequência.
As questões usando grandezas proporcionais costumam aparecer como problemas em que o cálculo é utilizado em alguma etapa ou cobrindo diretamente a relação entre grandezas.
Os gráficos não aparecem apenas na prova de Matemática e suas Tecnologias, mas eles são muito mais expressivos nesta prova.
É pedida a interpretação deles e de tabelas também, mesmo que eles sejam apenas uma das etapas da resolução da questão. Por isso, é um assunto para se ter na ponta da língua.
Além disso, também aparecem cálculo de média, moda e mediana.
🔵 Leia também: Conjuntos numéricos: resumo para se dar bem em Matemática no Enem
A aritmética contempla operações numéricas, e na prova de Matemática e suas Tecnologias, você encontra questões com cálculos simples e complexos.
Eles costumam envolver frações e números decimais, além de problemas relacionados com princípio da contagem, que aparecerem bastante também.
Porcentagem é mais um conteúdo que merece sua atenção nos estudos. Porcentagem é uma razão entre dois números com base 100. Seu símbolo principal é %.
As questões de porcentagem no Enem são cada vez mais frequentes e sua resolução envolve cálculos curtos, podendo ser utilizada a regra de três.
É comum que essas questões também envolvam muita interpretação.
🔵 Leia também: Exercícios sobre notação científica
Outro assunto recorrente é a geometria plana e espacial. Você precisará saber calcular a área de figuras e o volume de sólidos geométricos.
Também podem aparecer questões sobre visão espacial, planificações, teorema de Pitágoras e cálculo de perímetro.
Como esperado, as funções também aparecem com frequência na prova de Matemática e suas Tecnologias.
Elas aparecem como função afim, exponencial, logarítmica e quadrática, além da lei de formação da função e seu gráfico.
Análise combinatória é um conteúdo bastante recorrente no Enem.
No exame, é comum que seja cobrado em questões que envolvem princípio multiplicativo e agrupamentos (permutação, combinação e arranjo).
Normalmente, esse conteúdo é cobrado em questões que se relacionam com o dia a dia, como jogos de loteria ou no estudo das probabilidades, genética, entre outras aplicações.
🔵 Leia também: O que cai de Análise Combinatória no Enem?
Por fim, a probabilidade também é um conteúdo recorrente.
Para resolver as questões sobre esse assunto é preciso saber as fórmulas de probabilidade, mas também como aplicá-las dentro do que é pedido pelo enunciado.
A Matemática Financeira no Enem é cobrada de forma semelhante das provas dos vestibulares e concursos.
Os assuntos relacionados à Matemática Financeira são: porcentagem, acréscimo, desconto, operação de compra e venda, lucro, prejuízo, juros simples e juros compostos.
Agora que você sabe o que mais cai em matemática no Enem, já pode começar a montar um calendário de estudos. Vamos deixar algumas dicas que podem ajudá-lo:
🔵 Leia também: Como se preparar para as provas de Exatas do Enem
A prova de matemática do Enem não exige o conhecimento de muitas fórmulas, afinal grande parte das questões envolve muito mais raciocínio lógico e interpretação.
Contudo, existem determinadas fórmulas que podem ser muito úteis para essa etapa do exame. Confira quais são:
Cn,p = n! / p!(n – p)!
sendo n a quantidade de elementos de um conjunto e p, o número de elementos que serão combinados por vez.
As fórmulas mais importantes são a área do retângulo, que pode ser calculada multiplicando-se a base (b) pela altura (h), isto é, a = b.h, e a do triângulo, que sempre será a metade da área do retângulo: A = b·h/2
J = C × i × t
Sendo J = juros simples; C = capital inicial; i = taxa de juros; t = tempo da aplicação.
🔵 Leia também: As fórmulas de matemática mais importantes para o Enem
A primeira coisa a se dizer sobre isso é que não saber resolver uma questão de matemática é bastante comum e normal de acontecer no Enem.
A prova é extensa, cansativa e pode ser difícil lembrar de tudo. Por isso, é importante lembrar de manter a calma para pensar com clareza.
Se você não sabe como resolver uma questão, pule-a e volte a ela quando terminar as outras. Não vale a pena perder tempo em uma questão que você não sabe resolver.
Lembre-se que o tempo é um fator crucial no Enem.
Quando você tiver respondido todas que sabe resolver, volte para aquelas com as quais teve dificuldade e comece um processo de eliminação.
Leia o enunciado da questão novamente e elimine as alternativas que você tem certeza que estão erradas. Dessa forma, a probabilidade de escolher a alternativa certa aumenta.
Fique atento também nas semelhanças, repetições e oposições nas respostas, elas podem dar muitas dicas sobre qual é a alternativa certa.
🔵 Leia também: Como interpretar questões de matemática do Enem

Nós reunimos aqui algumas das questões de Matemática e suas Tecnologias que já caíram no Enem para você treinar. As respostas, você encontra na conclusão deste artigo.
Às 17 h 15 min começa uma forte chuva, que cai com intensidade constante. Uma piscina em forma de um paralelepípedo retângulo, que se encontrava inicialmente vazia, começa a acumular a água da chuva e, às 18 horas, o nível da água em seu interior alcança 20 cm de altura.
Nesse instante, é aberto o registro que libera o escoamento da água por um ralo localizado no fundo dessa piscina, cuja vazão é constante. Às 18 h 40 min a chuva cessa e, nesse exato instante, o nível da água na piscina baixou para 15 cm.
O instante em que a água dessa piscina terminar de escoar completamente está compreendido entre:
a) 19 h 30 min e 20 h 10 min
b) 19 h 20 min e 19 h 30 min
c) 19 h 10 min e 19 h 20 min
d) 19 h e 19 h 10 min
e) 18 h 40 min e 19 h
Dois reservatórios A e B são alimentados por bombas distintas por um período de 20 h. A quantidade de água contida em cada reservatório nesse período pode ser visualizada na figura.
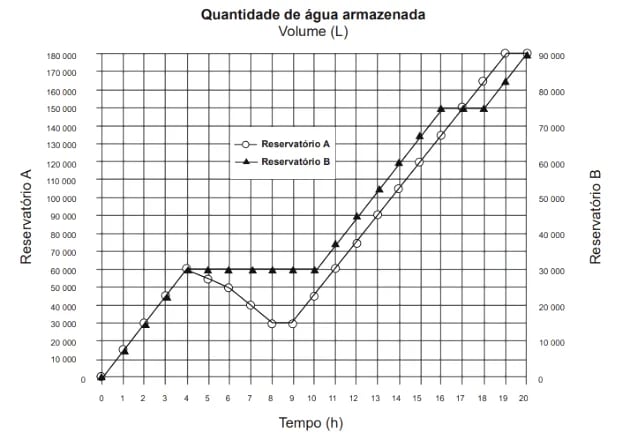
O número de horas em que os dois reservatórios contêm a mesma quantidade de água é:
a) 1.
b) 2.
c) 4.
d) 5.
e) 6.
Em um parque há dois mirantes de alturas distintas que são acessados por elevador panorâmico. O topo do mirante 1 é acessado pelo elevador 1, enquanto o topo do mirante 2 é acessado pelo elevador 2. Eles encontram-se a uma distância possível de ser percorrida a pé, e entre os mirantes há um teleférico que os liga que pode ou não ser utilizado pelo visitante.
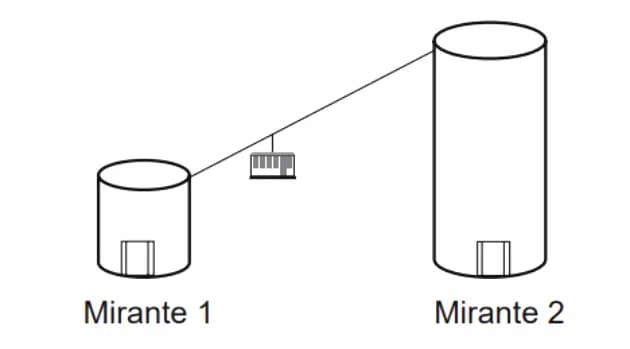
O acesso aos elevadores tem os seguintes custos:
O custo da passagem do teleférico partindo do topo do mirante 1 para o topo do mirante 2 é de R$ 2,00, e do topo do mirante 2 para o topo do mirante 1 é de R$ 2,50.
Qual é o menor custo, em real, para uma pessoa visitar os topos dos dois mirantes e retornar ao solo?
a) 2,25
b) 3,90
c) 4,35
d) 4,40
e) 4,45
Um garçom precisa escolher uma bandeja de base retangular para servir quatro taças de espumante que precisam ser dispostas em uma única fileira, paralela ao lado maior da bandeja, e com suas bases totalmente apoiadas na bandeja. A base e a borda superior das taças são círculos de raio 4 cm e 5 cm, respectivamente.
A bandeja a ser escolhida deverá ter uma área mínima, em centímetro quadrado, igual a
a) 192.
b) 300.
c) 304.
d) 320.
e) 400.
Para realizar a viagem dos sonhos, uma pessoa precisava fazer um empréstimo no valor de R$ 5 000,00. Para pagar as prestações, dispõe de, no máximo, R$ 400,00 mensais. Para esse valor de empréstimo, o valor da prestação (P) é calculado em função do número de prestações (n) segundo a fórmula

Se necessário, utilize 0,005 como aproximação para log 1,013; 2,602 como aproximação para log 400; 2,525 como aproximação para log 335.
De acordo com a fórmula dada, o menor número de parcelas cujos valores não comprometem o limite definido pela pessoa é pela pessoa é:
a) 12.
b) 14.
c) 15.
d) 16.
e) 17.
Um morador da região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso não chova, sua probabilidade de atraso é de 25%. Para um determinado dia, o serviço de meteorologia estima de 30% a probabilidade da ocorrência de chuva nessa região.
Qual é a probabilidade de esse morador se atrasar para o serviço no dia para o qual foi dada a estimativa de chuva?
a) 0,075
b) 0,150
c) 0,325
d) 0,600
e) 0,800
Esperamos que, ao chegar ao final deste artigo, as matérias que mais caem na prova de Matemática e suas Tecnologias do Enem tenham ficado mais claras para você.
Como prometido, confira aqui o gabarito das questões:
Bons estudos!
2023 © BLOG DO EAD | Todos os Direitos Reservados